Siempre que enseño osmosis realizo la típica actividad práctica de remojar patatas (y otras hortalizas) en soluciones de distinta concentración de soluto. Se cortan en bloques de tamaño y forma similares, se pesan y se dejan en remojo durante 24 horas. En la clase con mis alumnos, la diferencia de tamaño de los bloques es visualmente sorprendente. Pero, la dificultad viene a la hora de entender un gráfico de los resultados. Este es un post sobre cómo resolver este problema con una clase de alumnos de 16 años.
He aquí un gráfico de nuestros resultados (perdón por el eje Y torcido):
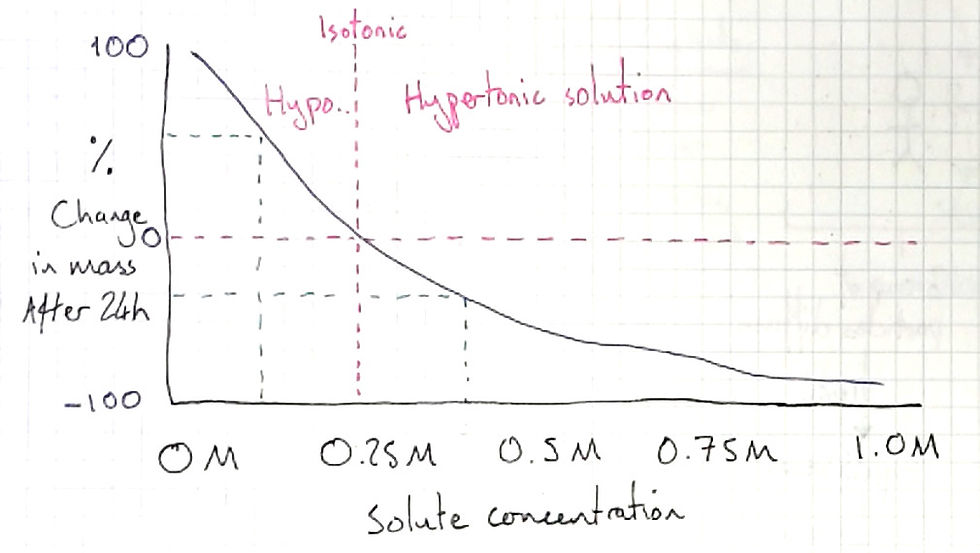
Al menos en mi experiencia, muchos alumnos tienen problemas para interpretar el gráfico porque lo confunden con un gráfico temporal. Ven el cambio de masa de los bloques de patata a lo largo del tiempo y, a pesar de que les explico explícitamente que el eje x es diferente, no pueden quitarse la idea de la cabeza.
Tienen que percibir la diferencia y hacer la distinción ellos mismos.
Por eso, siempre yuxtapongo el gráfico con un gráfico temporal, es decir, con el mismo eje y (porcentaje de cambio de masa) pero un eje x diferente. Pido a los alumnos que dibujen el gráfico justo debajo del otro gráfico y con los ejes del mismo tamaño (véase la imagen final de la lección, más abajo). Les digo que la escala de tiempo está entre los dos puntos en los que se pesaron (es decir, antes de ser puestos en remojo y después de 24 horas).
A continuación, les pido que predigan la forma de tres líneas para tres bloques de patatas:
En una solución hipotónica (mayor potencial hídrico)
En una solución isotónica (igual potencial hídrico)
En una solución hipertónica (menor potencial hídrico)
A continuación, les muestro mi respuesta y discutimos la diferencia entre su predicción y mi respuesta.
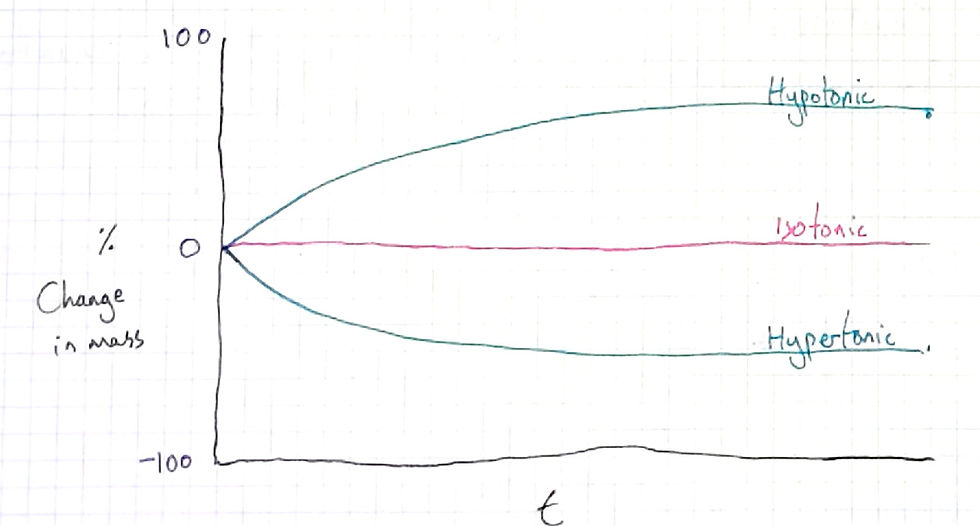
Mis alumnos suelen dibujar dos tipos de líneas: las rectas (no curvas) y las curvas (como las de arriba). Pero ninguno de los dos tipos de alumnos, según mi experiencia, puede explicar por qué han dibujado lo que han dibujado. Siempre parece que los alumnos que dibujan curvas como las mías simplemente se han acostumbrado a ver este patrón en los gráficos y lo esperan, sin conocer el mecanismo.
Así que aquí necesito un modelo de dinámica de sistemas para ayudarles. Lo bueno de los modelos de dinámica de sistemas es que puedes añadir y quitar componentes en función de lo que quieras que transmita el modelo. Por lo tanto no es la única forma de modelizarlo.
(Utilizo modelos de dinámica de sistemas con todas mis clases, con alumnos de 11 a 18 años).
En mi caso, quería un modelo que transmitiera el significado de las curvas del gráfico anterior. Si quieres ver cómo construyo modelos con los alumnos, consulta este post.
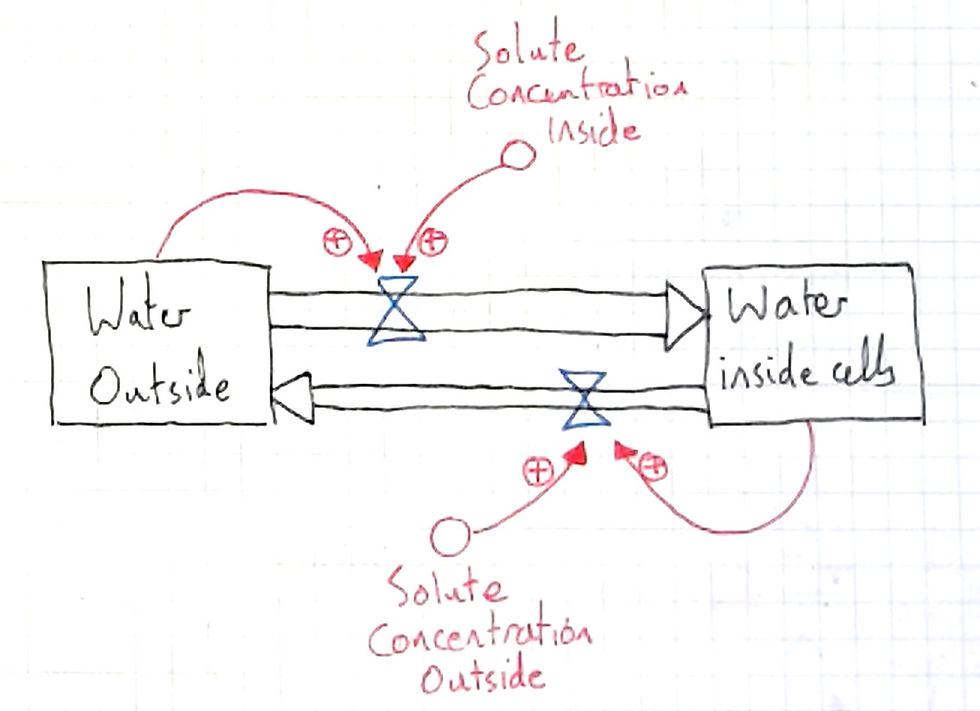
¿Qué muestra el modelo? En primer lugar, muestra cómo el flujo de agua que entra y sale de las células depende de la concentración de soluto. Empecemos con la existencia de "agua dentro de las células", observa cómo el flujo de salida de agua depende de la concentración de soluto en el exterior. La relación es "+", que significa "igual", lo que también significa que cuanto mayor sea la concentración de soluto en el exterior, mayor será el flujo de salida.
(Prefiero enseñar con el potencial hídrico, pero esta lección formaba parte de un programa que utilizaba la definición de soluto. Si fuera el potencial hídrico, la relación sería "-", que significa "opuesto", lo que también significa que cuanto menor sea el potencial hídrico en el exterior, mayor será el flujo de salida).
La salida de agua de las células se acumula en la reserva "agua exterior". En este modelo simplificado, existe una relación positiva (igual) entre esta acumulación y la entrada de agua de nuevo en las células. Esto puede considerarse como la presión del agua (que contribuye a aumentar el potencial hídrico).
A medida que mis alumnos y yo trabajamos el modelo en diálogo. Los alumnos llegan a ver que, a medida que el agua sale de las células, el factor de presión tiende a aumentar el agua que entra en la célula, hasta que se alcanza un equilibrio en los flujos. Cuando los alumnos piensan en estos factores simultáneamente, empiezan a ver el sentido de la curva del gráfico de tiempo de ósmosis anterior.
Después de percibir estas diferencias y hacer las distinciones, es el momento de volver al gráfico original del cambio porcentual en la masa frente a la concentración de soluto. Según mi experiencia, ahora los alumnos lo entienden mucho mejor y podemos discutir cómo podemos utilizarlo para estimar la concentración de solutos dentro de la patata y otras verduras.
Si te interesa saber cómo explico el mecanismo de la ósmosis, consulta este post.
Mis libros: Diagramas y Diálogo | Biología Hecha Realidad, o mis otros posts.
Descarga gratis los primeros capítulos de cada libro aquí.
Christian Moore-Anderson