In this post I will explain where I think many typical explanations fall short on the concept of surface area to volume ratio (SA:V) in upper secondary (ages 14-18), and my tips on how to solve them.
The parts and whole of the concept of SA:V
Typical explanations of SA:V in biology that I have seen (and done myself previously) go something like this:
Representations of cubes that get larger are shown with their measurements, which show how the volume increases quicker than the surface area. This ultimately restricts the size of cells. The restriction of cell size is often explained as an increase in the diffusion distance to the centre of the cell. The lesson then moves on to examples in human physiology of exchange surfaces which have large surface areas.
However, as such the concept has not been broken down sufficiently to its parts. Let me explain in four points:
Firstly: When presenting SA:V ratio with the typical cube example, two things are changing at once: Surface area and volume both change. According to Marton's variation theory (2014), students will be able to discern the pattern by firstly seeing the effect of changing one variable, before later changing the two a once.
Secondly: The cube example alone implies that volume is a major constraint on organisms, whereas it is really the SA:V. The emphasis should rather be placed on the change of SA:V and shape that organisms may experience through evolution over generations, or developmental and phenotypic plasticity during a lifetime.
Thirdly: There is confusion between the concept of SA:V in single cells, and in multicellular organisms. These two concepts need to be separated and explored independently.
Fourthly: While the increase in diffusion distance is a constraint on life, it is only one factor of a more encompassing concept. There needs to be sufficient surface area, to maintain sufficient exchange rates, to maintain the totality of living matter.
For example, a human born with only one lung will have less exchange surface, despite the circulatory system maintaining a short diffusion distance. Equally, an organism can lower its metabolic demand if increasing its SA:V is not possible or beneficial.
Its about maintaining a sufficient rate of flow of energy and matter relative to metabolic demand.
Teaching it: Begin with unicellular organisms in ecological context
An image from a youtube video by Journey to the Microcosmos
Why do these unicellular organisms have this shape?
Why not other shapes? Here I give students some time to just admire cells with a video from the Microcosmos. Because we should have just studied Fick's law, questioning can guide students towards these ideas.
A concrete analogy
Following these questions I do a demonstration I thought up a few years ago that involves the conduction of heat as an analogy for diffusion rates. For this, I have two pots of heat sensitive putty, so that both the same volume (don't mix them), and for better results, have them in the fridge before the lesson. One I shape as a sphere, and the other I squash into a rod (like a bacillus), while questioning for predictions and reasoning.
This is that heat sensitive putty stuff
I drop them both into 1 L beakers with some hot water. Using tongs, I pull them out immediately. I then slice them in half and students can clearly see the difference. The sphere maintains a larger 'cold' region.
This demonstration is important, because, in life, organisms will evolve, and develop, more or less surface area to match the demands of their living tissue. Not only this, but for efficient explanation I am only changing surface area (by changing shape), while maintaining volume constant.
Quantifying the example
I use a pre-made picture to quantify the effect on SA:V of changing shape but maintaining volume.
My picture for showing a change in SA:V when changing shape but not volume
And, I show another picture with more realistic unicellular shapes and sizes (with units):
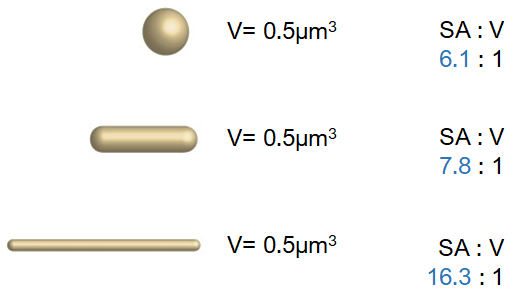
A picture I've edited for showing a change in SA:V when changing shape but not volume
Now we're ready for some ecological and evolutionary discussion using what I have called (in my paper) a trait-spectrum case (see my book). For example, the trait here is the cell shape, and spectrum extends from a sphere to a really skinny elongated cell.
This allows for discussion about omnipresent trade offs in life, due to ecological pressures. Too much, or too little of something might be disadvantageous; at what point is the trait most advantageous, where is the Goldilocks zone? It doesn't need to be super accurate, its purpose is to get students practising thinking and seeing problems like a biologist.
Trait-spectra are also important to avoid students gaining the idea of dichotomous traits (such as black or white, spherical or rod), as has been observed by Alred et al. (2019).
Is there a trade off with the morphology of the cell? If a larger surface area is better, why not form an incredibly elongated cell? You could discuss predation trade offs, and cell integration trade offs. It's possible here to use examples such as filamentous cyanobacteria; why don't they arrange into a sphere? Other examples of unicellular shapes can be found and discussed comparatively in the Microcosmos videos.
How about just having a larger cell?
Now I converge more with typical lesson explanations. Why don't these cells (whatever examples you've been looking at) just get bigger? Again another opportunity for discussion of ecological trade offs, with the most accessible point probably being predation and avoidance of it (like a stentor, a predatory cell that has an interesting shape and has to be large enough to be able to predate on others).
I introduce the cube example, in which both volume and surface area change at the same time.
My picture for showing the cube example of SA:V
From here, the discussion can move on from only the rate of flow of energy and matter, to incorporate how this knowledge of this rate is more useful when it is considered relative to the total living volume it is exchanging for.
The discussion needs to be contextualised. Cell sizes are limited yes, but species evolve and organisms show phenotypic plasticity: organismal morphology is typically not cube like, and shape is a very important variable for survival and reproduction.
Depending on the class, at this point I may look at some graphs of these variables, and practice some of the calculations of SA:V of cubes (which are the canonical examples found in exams). This may conclude the lesson, saving multicellular organisms for the next.
As the agar cube SA:V practical is so well known (because it's so good) I will not talk about it here.
Multicellular organisms
Understanding the parts and the whole of the concept
To jump from the cube example straight to exchange surfaces in humans (or other animal, plant) might be too fast. Firstly we need to discern the similarities and differences between unicellular and multicellular organisms.
All organisms share the requirement to maintain a SA:V that matches their metabolic demands. So morphology is as important for uni- as for multicellular organisms.
In multicellular organisms, individual cells of exchange surfaces often show adaptations for increasing their SA:V, such as the flattened shape of pneumocytes. However, it is important to distinguish this concept from where many cells function together providing extra surface area at the level of tissues and organs to provide for other cells of the body.
This is SA:V at multiple scales in multicellular organisms. But we're going to simplify it here to just two: the SA:V of the individual cells of exchange surfaces, and then how this relates to the SA:V of the whole organism.
While in unicellular organisms volume is simply what is found inside the cell membrane, in multicellular organisms volume constitutes all the living cells of the body, its biomass.
Teaching it in context
Now, this is where personal preference will come into play. Personally, I prefer to jump into the example of just one exchange surface and look at it in detail. The other examples will come in time as we proceed through the curriculum. Others, however, may prefer to show many examples together.
My favourite place to begin is the gas exchange system (the respiratory, or ventilation system). The reasons for this are several:
Firstly: The adaptations of pneumocytes and alveoli for gas exchange are simple and intuitive. If you begin with the intestine, you have to introduce microvilli, villi, and intestinal folding as your first example.
Secondly: The SA:V of the gas exchange system correlates well with the metabolic demand of the living biomass, mainly because animals typically hold negligent oxygen stores. Thus, it is much easier for the student to link the morphology of the lungs with the flow of energy and matter (in this case O2 intake and CO2 excretion rates).
With the digestive system there are more factors that muddy the water. We hold large stores of organic matter for later use. Furthermore in the digestive tract we have the processes of digestion, and egestion of organic matter that is not absorbed.
Trait-spectrum cases are easily discussed for the gas exchange system and SA:V, including trade offs between the flow of oxygen to power metabolism, and the energetic costs of maintaining the specialist structure, or the addition space required for it.
Thirdly: Related to the second point, the relative simplicity of the gas exchange system of humans compared to the multi-compartment digestive system, means that comparative biology is easier.
At it simplest, the lungs of humans (and mammals) can be compared to those of amphibians and reptiles, but this can easily be extended to other organisms. With the multiple examples students can begin to discern the core patterns of gas exchange, while the differing morphology can be used to enhance a discussion of their ecology and evolution. Why do amphibians have smaller lungs compared to mammals? Why don't they evolve a larger SA:V? et cetera.
An image I found on google
A final note
If you haven't already, do read Haldane's famous 'On being the right size'. For now, I will leave you with this single paragraph:
'A typical small animal, say a microscopic worm or rotifer, has a smooth skin through which all the oxygen it requires can soak in, a straight gut with sufficient surface to absorb its food, and a single kidney. Increase its dimensions tenfold in every direction, and its weight is increased a thousand times, so that if it to use its muscles as efficiently as its miniature counterpart, it will need a thousand times as much food and oxygen per day and will excrete a thousand times as much of waste products.'
My books: Difference Maker | Biology Made Real, or my other posts.
Download the first chapters of each book for free here.
References
Alred, A. R., Doherty, J. H., Hartley, L. M., Harris, C. B., & Dauer, J. M. 2019. Exploring student ideas about biological variation. International Journal of Science Education, 41(12), 1682–1700.
Marton, F. 2014. Necessary Conditions of Learning. London: Routledge.