A principle of variation theory is identifying the aspect you really want students to discern, and then varying it. Importantly, when you vary it, you must try to keep all other aspects invariant so that students notice what you want them to notice. Read a quick blog post on variation theory here.
In my view, to understand p-values, you must discern an important aspect: how confident you can be when interpreting data. To see that, the critical aspect to be aware of is seeing how the relationship between means and their spread of data can vary. And then how this affects your confidence in interpretation. This post isn't about the statistical how of p-values, but how students cna make meaning of them. Here's how I do it.
I begin by drawing a representation of sampling. This is a key concept, but students are often familiar with it in terms of their education and the exams they sit.
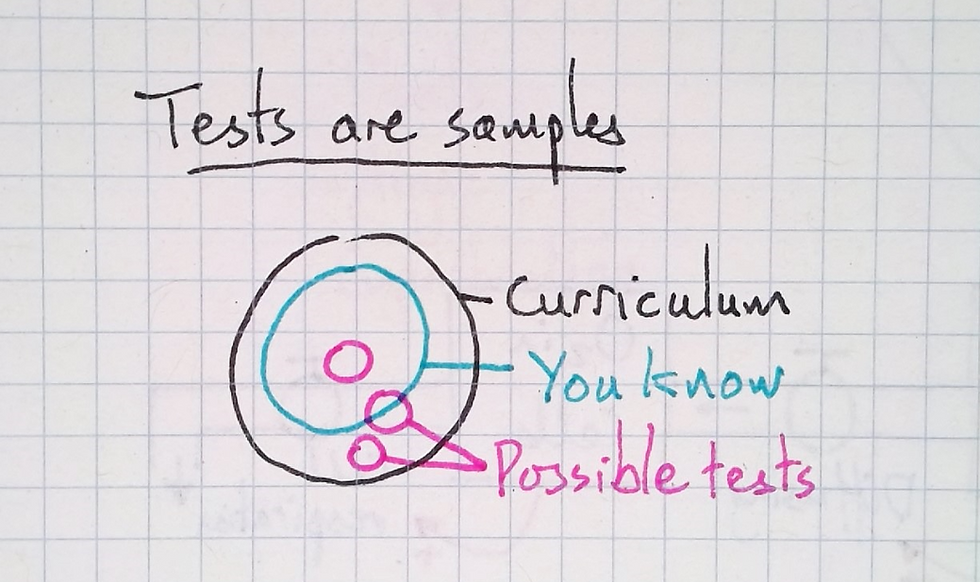
The largest circle represents all the information of a curriculum, the medium circle represents how much of this a student knows. The three smaller circles represent the knowledge that is sampled on any one test.
If you’re lucky a test samples the part of the curriculum you know, if you’re unlucky it’ll test everything you don’t know. Most of the time it’s somewhere in between. I ask students if it’s better to have a larger or smaller exam as a sample and they agree that a larger sample is less risky for them. I point out that it’s also more reliable as a measure of what they know.
Next I draw a bar chart representing two classes—studying the same course with the same teacher—and their test results. Both classes scored 50% on average. At this point I don't yet add the dots representing individuals, and I ask the students if the classes are exactly the same.
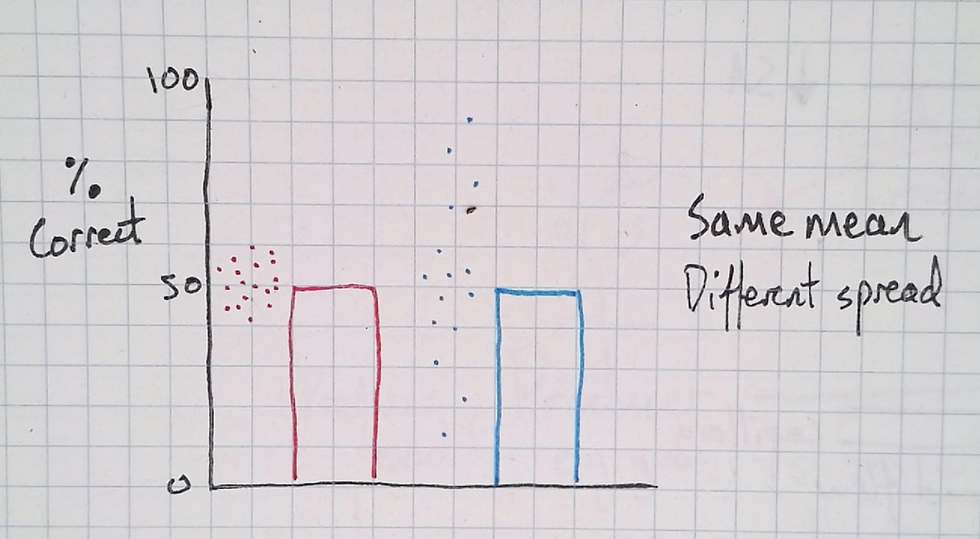
While some students suggest that they are, some students sometimes mention that one class might have more higher, and lower scorers than the other. I add this to the bar chart using dots to represent individual scores. One class has a spread of scores close to the mean, whereas the other has scores that are far more spread. This step has varied one thing. It has kept invariant the curriculum, the exam, and each class’ mean result. Only the spread of results has varied, and has therefore brought this to the attention of the students.
I then draw a bar chart with identical axes, and I say to students that in the same course, two other classes got these results:
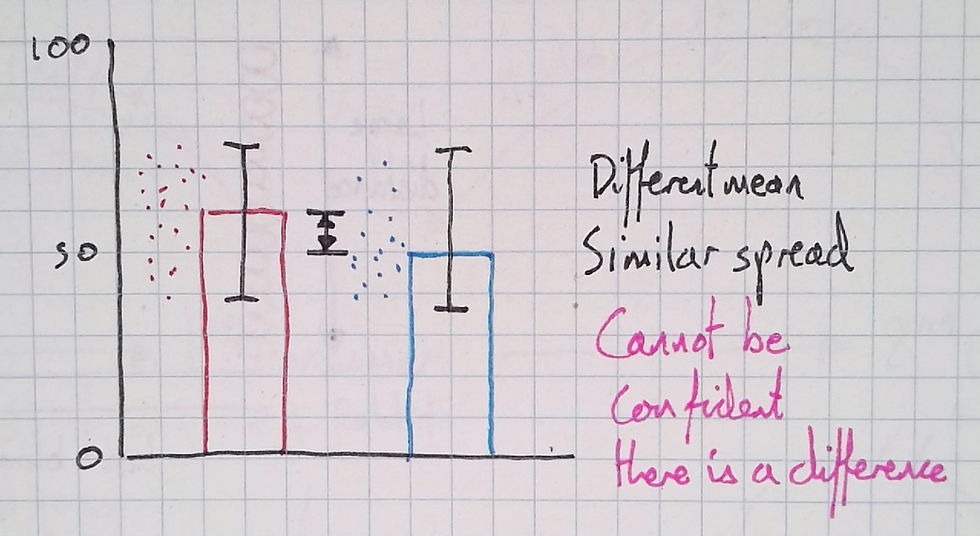
Now the means are different, and I draw dots to show a similar spread of results. As the means vary but the spread doesn't (much), it is brought to the students attention. (forgive the range bars here instead of standard deviation bars). I ask the students if the classes are different—does one class really know more than the other? To help them here, I also ask if they think one class would always come out better, on average, if I gave them five more tests to complete.
Crucially I ask them how confident they would be making a prediction. This is key to understanding P values, as P refers to probability. The students typically agree that they couldn’t be so confident that they’d keep getting the same difference between the classes in other tests. Therefore, the classes could be similar in how much they know.
I then draw another bar chart with identical axes. This time however, both the mean and the spread are different. The means represent 80% correct for one class, and just 30% for the other. And the individual results of each class are no way near each other—there is no overlap.
I then repeat the question to the student about how confident they are that the two classes are different in how much they know. I use the same question of what would happen if I gave them five more tests. The students typically express that they would be very confident that they could predict the result.
Next, I give students a heuristic for interpreting graphs with error bars. I draw the error bar examples one by one and ask students if they would assume that it was a real difference. The a rough rule of thumb I give them is to only assume a difference if the error bars do not overlap at all, but to remember that this is an assumption only. In fact, some would give a stricter rule.
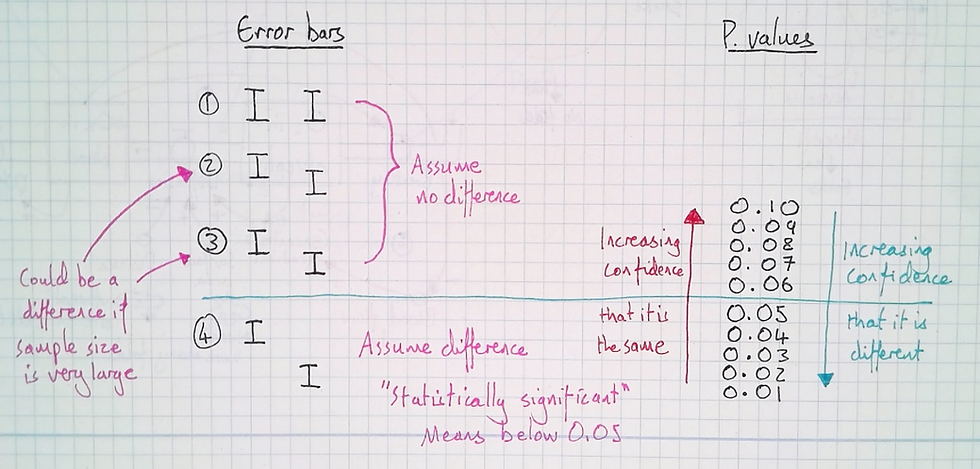
I also give them the exception that with very large sample sizes error bars may overlap and still represent a difference. On their assumption, they should seek better verification of how confident they can be. Here then, I introduce the idea of the p-value, and tell them that many different statistical tests will give a p-value, a number that indicates a statistical level of confidence. Not a magnitude of difference, but a level of confidence you can assume that there is a difference.
I finish the lesson by discussing the typically acceptable p-values—below 0.05—is the standard for being confident enough to assume a difference. Higher than this number you should be more inclined to assume similarity. In biology, as data is messier, a p-value of 0.05 is more acceptable than in physics in which systems being observed are simpler and can be controlled with precision.
Finally I discuss the problems that arise when scientific journals prefer to only publish papers with p-values below 0.05, which incentivises p-hacking, and the loss of information about experiments that reveal similarity rather than difference.
And If you've liked this then check out my book, which is based on variation theory. Download chapter 1 here—English edition—edición española—or check out my other posts.
@CMooreAnderson (Blue Sky)
@CMooreAnderson (X)
